札幌のチャットレディは
容姿年齢関係無く
お仕事出来るって本当!?


業界初!


ちょこ札幌でお仕事する方全員が、待機中やチャット中などのお仕事中に
ちょこ札幌の激盛りWEBカメラを使用できます!
ちょこ札幌でお仕事する方全員が、
待機中やチャット中などのお仕事中に
ちょこ札幌の激盛りWEBカメラを
使用できます!
チャットレディプロダクションちょこ札幌の激盛りWEBカメラは、 各ライブチャットサイトで、自身のお顔を『盛れる』で有名なSODAやSNOWやUlikeなどのアプリと同じく輪郭・目の大きさ・目の位置などを調整し、 誰でも芸能人並になれます。
市販のWEBカメラでお仕事するより、 お客さんに気に入ってもらえる確率がグッと高まり、固定のファンがどんどん増えます。
当社へ移籍した他社経験者をもとに平均を出した所、ちょこ札幌は約5倍稼ぐことができるという結果となりました!!!
また、別人としてお仕事するので身バレ対策にも安心です。
※激盛りWEBカメラは、ちょこ札幌でしか使えません。同様の表現の代理店にご注意下さい。


ちょこ札幌でお仕事する方全員へ、出勤時や待機中などお仕事中や合間に
専属メイクアップアーティストがメイクアップ!
ちょこ札幌でお仕事する方全員へ、
出勤時や待機中などお仕事中や合間に
専属メイクアップアーティストが
メイクアップ!
さらに!札幌のチャットレディ事務所の中では、屈指の実力を誇る、専属メイクアップアーティストによる『カウンセリング』・『ヘアスタイリング』・『メイクアップ』が受けられます。
ちょこ札幌限定の激盛りWEBカメラと合わせれば、モデルやタレント顔負けの容姿でお仕事可能!その効果は、以下の動画をご覧下さい。
別人のように変身していくのがわかりませんか?魔法みたいですね♪
容姿に自信が無くて、他のお店であまり稼げていない方も、是非、ちょこ札幌でお仕事してみて下さい。月収100万円以上が、現実になりますよ。
また、ちょこ札幌では、メイクアップアーティストによるメイク加工動画をシリーズ化して、YoutbeやTikTok、Instagramにfacebook、Twitterなど、各種SNSで公開しています。どんどん追加していくので、こちらもお楽しみに!
☆撮影モデル募集中☆
モデルのみのお仕事もOK☆詳しくは
お問い合わせください。
札幌のチャットレディ
はギガ級報酬!





札幌のチャットレディプロダクションちょこ札幌では、月収30万以上が50%以上!100万以上も多数います。
札幌のチャットレディ
プロダクションちょこ札幌では、月収30万以上が50%以上!
100万以上も多数います。

- ちょこカメラ採用
- 完全全額
日払い - 高額
ボーナス
あり
高収入アルバイトと言われるチャットレディの報酬は、男性の会員様と話した時間が1分単位で課金されます。
ちょこ札幌は、業界最高峰の報酬額!
完全日払い制で、高額ボーナスも多数ご用意しております!
明確報酬!リアルタイム報酬確認ができるのは、ちょこ札幌だけ♪


札幌のチャットレディ
はサービス多数!



Point.1 個人情報管理士のスタッフが在籍!デジサートサイトシールも取得!
チャットレディプロダクションちょこ札幌では、個人情報管理の資格を持ったスタッフの監督のもと、個人情報については厳重に取り扱っています。
2017年5月30日より、個人情報保護に関する法律が施行されましたので個人情報管理士の資格を持ったスタッフがいる事務所だと安心してお仕事ができます。
また、堅牢なセキュリティ対策を行っている証となる、デジサートサイトシールを取得致しました。こちらは、札幌のチャットレディプロダクションでは初となります。
※個人情報管理士の在籍していない代理店にご注意ください。
※マイナンバーを控える事はございません。
本人確認の為であっても他人にマイナンバーを教えることは禁止されています。
個人情報は個人情報管理士指導の元で厳重に管理致しますのでご安心くださいませ。
【個人情報管理士とは】
個人情報保護・管理に関する法律・各省庁のガイドライン、業界のガイドライン、
都道府県の個人情報に関する条例、JIS Q 15001の知識を有し、企業・団体(個人)において個人情報保護・管理、有効活用・運用を
適切に行うことのできるエキスパートの事を指します。
出典:一般社団法人 日本個人情報管理協会より
【デジサートサイトシールとは】
デジサートサイトシール(デジサートデザイン)は、ウェブサイト運営者の実在性及び、
セキュリティの安全性、信頼性を示すマークです。
単なる画像でなく、コピーできない仕様となっており、本WEBサイトについて、サイトとサイト運営企業を公的証明致します。
「デジサート」は、米国のデジタル証明書(SSL/TLS)の認証局を運営する世界最大手の企業です。ウィキペディアやFacebook、ソニー、トヨタ
などのWEBサイトもデジサートによる電子証明書の認証を受けており、確かな信頼性を担保します。
出典:digisert公式サイトより
※マイナンバーを控える事はございません。
本人確認の為であっても他人にマイナンバーを教えることは禁止されています。
個人情報は個人情報管理士指導の元で厳重に管理致しますのでご安心くださいませ。
【個人情報管理士とは】
個人情報保護・管理に関する法律・各省庁のガイドライン、業界のガイドライン、
都道府県の個人情報に関する条例、JIS Q 15001の知識を有し、企業・団体(個人)において個人情報保護・管理、有効活用・運用を
適切に行うことのできるエキスパートの事を指します。
出典:一般社団法人 日本個人情報管理協会より
【デジサートサイトシールとは】
デジサートサイトシール(デジサートデザイン)は、ウェブサイト運営者の実在性及び、
セキュリティの安全性、信頼性を示すマークです。単なる画像でなく、コピーできない仕様となっており、本WEBサイトについて、
サイトとサイト運営企業を公的証明致します。「デジサート」は、米国のデジタル証明書(SSL/TLS)の認証局を運営する世界最大手の
企業です。ウィキペディアやFacebook、ソニー、トヨタなどのWEBサイトもデジサートによる電子証明書の認証を受けており、確かな信頼性を担保します。
出典:digisert公式サイトより



Point.2 完全自由出勤制・在宅勤務もOK
ちょこ札幌は、24時間完全自由出勤制となっております。「朝8時からお仕事したい」「夜中の3時からお仕事したいな…」「今、時間が空いたからお仕事したい!」これら全てOKです。
「今日は丸1日時間が空いてるから、フルでお仕事して高収入を目指そう!」や「1時間しか時間ないけど少しでもお仕事したい!」なんて事だってOKです。
また、お仕事やご家庭の事情などで急に出勤できなくなってもペナルティなどは一切ございません!

Point.3 完全防音個室を採用
落ち着いてお仕事していただくために、札幌の各オフィスに1人1防音室をご用意しております。
各個室の防音性能は、一般的な壁に使われる建材の石膏ボード以外に、スピーカーのウーファーに使われるMDFなどの材質を用いて製作しております。
また扉には、二重の空気層を設けたドアを採用しており、より防音効果を発揮します。
チャットレディには安心の防音に特化した設計となっております。

Point.4 全国売上上位チャットレディをプロデュースしたスタッフが在籍
ちょこ札幌では月収200万円を超える、全国売上上位チャットレディをプロデュースしているスタッフが在籍しております。
また、数多くのリピーターとなるお客さんを獲得できるノウハウをアドバイスしております。
チャットレディのお仕事で1日に1人のリピーターを掴む事ができれば10日で10人です。
リピーターが増えるということは、もちろん報酬アップに直結します。
減ってしまう事があっても、続けていけば、結果的にはプラスとなり、月収200万を超える事が可能となります。札幌で屈指の実績とノウハウを、是非ご利用下さいませ。

Point.5 送迎サービスあり
チャットレディのお仕事の終わりには、担当スタッフが、安全にご自宅まで送り迎えをしております。札幌全域から、郊外までカバーしておりますので、お気軽にご利用下さいませ。



- 面接交通費
2,000円
支給 - うれしい
入店祝金
最大10万 - 報酬最大
+212,000円
ボーナス
札幌のチャットレディ
の皆さんの
要望って?



時間に縛られず、自由に出勤したい!

待っている時間も時給が欲しい!

ノルマや罰金にしばられたくない!

お金をいっぱい稼ぎたい!

周りを気にしなくていい個室で働きたい!

容姿に自信がないけど働いてみたい!


新着情報
INFORMATION
- - チャットレディに札幌でもおススメの理想のお部屋の背景や部屋作りとは?【ブログ更新】
- - 札幌のチャットレディにボーナスってあるの?ボーナスを意識してモチベーションアップ♪【ブログ更新】
- - チャットレディは札幌でもどんな下着を身につけるのが男性ウケして稼ぎやすいの?【ブログ更新】
- - 札幌でチャットレディは未経験でも稼げる!まずは通勤チャットレディから始めよう!【ブログ更新】
- - チャットレディが札幌の主婦におススメ!自身の時間に合わせて柔軟にお仕事して収入にも満足出来る♪【ブログ更新】
- - 札幌のチャットレディが知っておきたいお礼メールの基礎【ブログ更新】
- - 札幌で報酬をあげるためにチャットレディが持っておきたい接客スキルとは?【ブログ更新】
- - チャットレディの札幌での生活リズムはどうなってる?リズムを正すための方法とは【ブログ更新】
- - 札幌でもチャットレディがインボイス制度導入で知っておくべきこととは?その②【ブログ更新】
- - 札幌でもチャットレディがインボイス制度導入で知っておくべきこととは?その①【ブログ更新】
チャットレディプロダクション
ちょこ札幌の
お仕事内容

パソコンに接続してあるWEBカメラを通して、男性会員様とチャットでお話して頂く簡単なお仕事です。
キーボードを打つのが苦手な方も、マイクを使えば、タイピングをすることなく安心してお仕事ができます。
実際多くの人が、キーボードよりマイクを使って、楽しくチャットをしています。
チャットレディプロダクション
ちょこ札幌の
報酬形態
高収入アルバイトと言われるチャットレディの報酬は、男性と話した時間が1分単位で課金されます。
また、2ショットチャットか、パーティーチャットかによっても変わってきます。
2ショットチャット

・お客様1人を接客していただきます。
・1:1での接客状態。
2ショットチャットの1時間のお給料
パーティーチャット
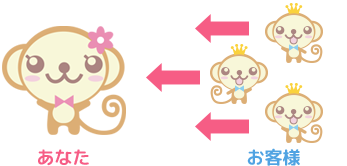
・複数のお客様を接客できる状態。
・お客様全員分が報酬に加算されます。
複数のお客様を接客している時の
1時間のお給料は?※一例
チャットレディプロダクション
ちょこ札幌の
応募からお給料までの流れ

最短60分でお仕事開始!
もちろんゆっくり稼げる
コツなどもお話します。
Step.1 応募!
お電話・WEB・LINEいずれか、ご希望の方法でお気軽にお申し込みください。

Step.2 お仕事説明
チャットレディ経験やノウハウのあるスタッフが、丁寧に仕事内容を説明いたします。不明や不安なことは何でもお尋ねください。

Step.3 お仕事スタート
面接後、当日からチャットレディとしてお仕事することも可能です。

Step.4 お給料GET
お仕事終了後、完全日払いでお給料をお支払いいたします。

当店の面接はお仕事説明がメインとなります!
応募された方全員採用となります。
簡単なお仕事の説明と登録作業ですので気軽にお仕事開始できます!
当店の面接はお仕事説明がメインとなります!
応募された方全員採用となります。
簡単なお仕事の説明と登録作業ですので気軽にお仕事開始できます!



札幌のチャットレディ
プロダクションの中で
選ばれる
3つの理由とは!?


![]()

毎月ボーナス10万円以上

参加サイト10サイト以上!報酬額が高い!

待機保障アリ

ノルマや罰金一切無し!

全国売上ランキング上位者在籍!

完全自由出勤制・在宅勤務もOK!

完全個室制!チャットルーム100部屋以上

送迎サービスあり
プロフ写真撮影あり

- プロフ写真は、とっても重要です!ちょこ札幌では、撮り慣れたスタッフが、あなたをかわいく魅せるプロフィール写真を撮影しています。
衣装完備

- チャットをもっと楽しむために、たくさんのかわいい衣装をご用意しています。着替えると、いつもと違う自分になれて、会話もはずむかも!?
ちょこ札幌カメラで理想の自分に大変身!

- ちょこ札幌激盛りWEBカメラは、 各ライブチャットサイトで、自身のお顔を『盛れる』 で有名なSNOWやBeautyPlusやUlikeなどのアプリと同じく小顔・美白・デカ目などを調整し、誰でも芸能人並になれます。
便利にお買物!ショッピングモール

- オンラインで買い物できるちょこ札幌のショッピングモールでは、「あったらいいな~」という商品を取り揃えております。チャットの休憩時間や、PC前から動けない時に、チャットルームから注文できるので便利です。
簡単操作システム

- PCの操作がわからなくなった時や相談事がある時など、ボタン1つでスタッフを呼び出すことができます。お仕事終了後の清算も、ボタン1つで簡単です!
美肌!フロントライト

- 女の子を美しく魅せるために、照明にもこだわり、プリクラ機に搭載されているフロントライトを設置しました。照明効果で、あなたの美肌を最大限までひきだします!
ウィッグご用意しております

- ちょこ札幌では、豊富にウィッグをご用意しているので、いつもと違う自分を演出できます!
![]()


- 面接交通費
2,000円
支給 - うれしい
入店祝金
最大10万 - 報酬最大
+212,000円
ボーナス
チャットレディプロダクション
ちょこ札幌の
チャットレディの声と1日の流れ

VOICE.01るるちゃん
友達などにかわいくなったねと褒められることが多くなりました。
チャットレディは報酬面だけではなく、プライベートも充実できるようになる職業だと思います。また、違う自分になってお仕事してみると自分の知らなかった自分を見つけることが出来る職業だと思います。
 事務所に訪れる。
事務所に訪れる。- ▼
 メイクや着替えをします。
メイクや着替えをします。- ▼
 きれいな姿になってお仕事。
きれいな姿になってお仕事。- ▼
 送迎車でラクラク帰宅。
送迎車でラクラク帰宅。
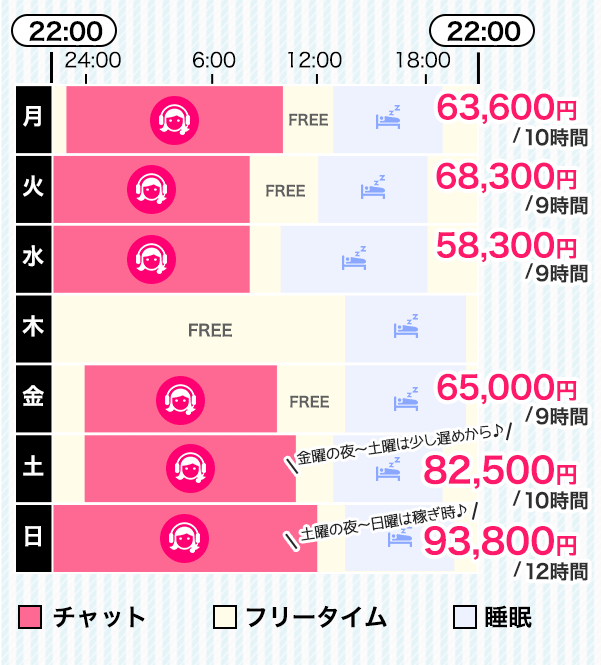
るるちゃんの1週間



VOICE.02まいちゃん
ノルマや強制は無く、ボーナスがもらえることも続けている一因です♪
ちょこ札幌は、事務所の場所が通いやすくてとってもいいです。みんな親切に接してくれます。ノルマもないし強制もされないので働きやすいです。あと、ボーナスがもらえることも、続けていこうと思える一因です。
まいちゃんの1週間



VOICE.03あいちゃん
本業の二倍稼ぐ事を目標にしています!
ちょこ札幌さんではかわいい衣装を貸し出して下さり普段着たかったけど、着れない服が着れて嬉しいです。また、選ぶ際にもスタッフさんがアドバイスしてくださり、男ウケの良い服装を知ってプライベートでも取り入れちゃいました!(笑)
あいちゃんの1週間




VOICE.04れなちゃん
完全自由出勤で完全日払い制なところも、働きやすくて気に入っています。
ちょこ札幌で継続している理由は、頑張ったら頑張った分だけたくさんのボーナスがもらえるし、環境がとても良いし、何よりここのスタッフがみんな良い人だから!完全自由出勤で完全日払い制なところも、働きやすく気に入っています。
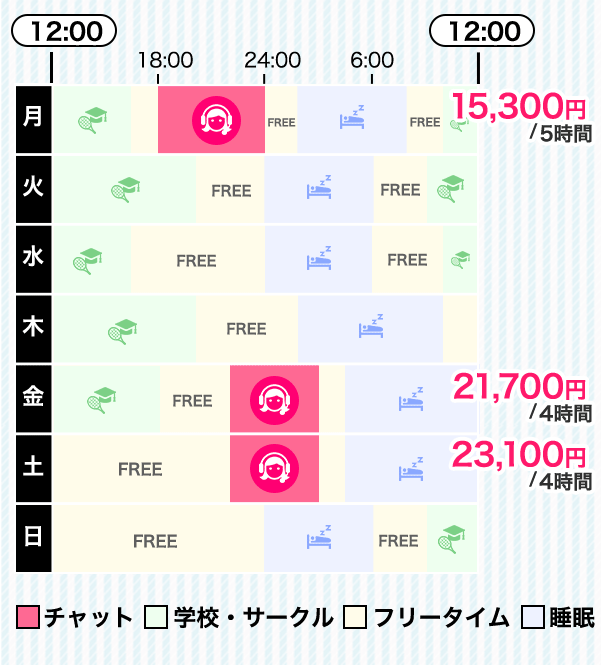
れなちゃんの1週間



VOICE.05みおちゃん
親身になって相談にのってくれるし、いつでも何でも聞きやすい雰囲気です。
スタッフさんも気軽に声をかけてくれたり、声をかけたりできるようなアットホームな場所なので、長く続けることができています。
みおちゃんの1週間






札幌のチャットレディの間で特に
質問が多い物の回答集!
- Q.チャットレディの経験がないのですが、大丈夫ですか?
- A.チャットレディのお仕事は完全歩合制のお仕事となっております。
一概にいくらという回答は難しいのですが、当社の平均として時給換算すると4,000~5,000円程となっております。
接客次第では時給換算で1時間あたり30,000円以上稼ぐ事も可能なお仕事です。
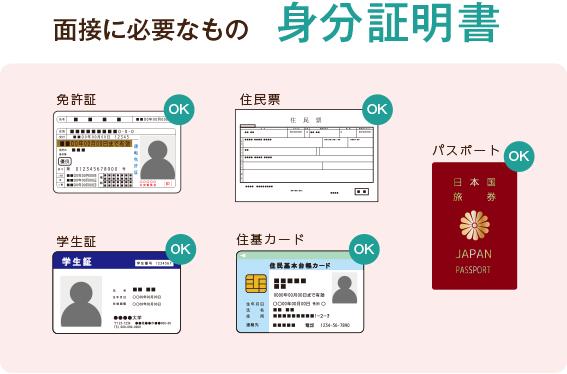
- Q.面接時に必要なものはありますか?
- A.
- Q.登録の際、容姿の選考基準はありますか?
- A.登録に関して、容姿は一切関係ございません。 男性会員様には様々な趣味嗜好の方がいます。
また、容姿に自信がなくても「メイクアップアーティストによるメイク」と「ちょこ札幌激盛りWEBカメラ」を使用することで誰でも芸能人並に可愛くなれます!
自分では短所と感じられたポイントが他人には長所であることもあります。
自信を持って登録して下さい。
- Q.面接は、どのような内容ですか?
- A.面接では、お仕事の説明や、サイトの登録方法をご説明しております。面接時に、稼げるコツをお伝えしているので、その日からでもお仕事が可能です。
- Q.経験者なのですが移籍は出来ますか?
- A.はい可能です。
ちょこ札幌は移籍OKとなっております。ちょこ札幌が導入している専属のメイクアップアーティストによるメイクと激盛WEBカメラによる加工が非常に好評なため、他社さんからちょこ札幌へ移籍し、最終的にちょこ札幌に籍を残して頂ける方がとても多く、皆さまには感謝しております。
ご検討中の方は、是非お気軽にご連絡下さい。
- Q.勤務地と時間帯についてはどのようになっていますか?
- A. ☆通勤型の場合(24時間営業)
本社は、すすきの駅より徒歩1分&豊水すすきの駅徒歩3分の、交通の便のよいところにあります。
札幌市中央区南3条西3丁目6-2 TM24ビルディング3階 になります。
他にも札幌市内や東京・大阪に店舗が複数あります。
・札幌駅前店
・大通り店
・市電資生館小学校前駅付近 (南5西6)
・地下鉄豊水すすきの駅付近 (南6東1)
・麻生店
・琴似店
・清田店
・北24条店
・手稲店
・東京都池袋店
・大阪市大阪梅田店
・(2023年OPEN!)仙台店
・(2023年OPEN!)千葉店
ご希望であれば、送迎サービスや、お迎えサービスもご用意しております。
☆在宅型の場合
インターネットに接続できる環境とパソコン・カメラがあれば24時間いつでも参加可能です。
また、スマートフォンからもお仕事可能です。お気軽にお問い合わせください。
チャットレディプロダクション
ちょこ札幌
ってどんな会社?
![]()
札幌市内に10店舗、東京に1店舗、大阪に1店舗ある運営年数の長い大手会社です!
本社は、すすきの駅より徒歩1分&豊水すすきの駅徒歩3分の、交通の便のよいところにあります。
札幌市中央区南3条西3丁目6-2 TM24ビルディング3階 になります。
・札幌駅前店
・大通り店
・市電資生館小学校前駅付近 (南5西6)
・地下鉄豊水すすきの駅付近 (南6東1)
・麻生店
・琴似店
・清田店
・北24条店
・手稲店
・東京都池袋店
・大阪市大阪梅田店
・(2023年OPEN!)仙台店
・(2023年OPEN!)千葉店
札幌市内で大人気のチャットレディプロダクションです。
日々、女の子の働きやすい環境を考えて、スタッフ指導やサポートを徹底しています。
また、高収入チャットレディプロダクションちょこ札幌は、株式会社として経営している会社です。
ライブチャットルーム運営は大半が風俗との兼業ですが、当社は広告代理業、ホワイトニング事業、パソコン販売、防音室事業の業務を兼業しています。
働く女性に他業種の仕事を勧誘・斡旋することはありません。
また個人情報などの守秘義務も完璧です。
オフィスはどんなところ?
札幌のチャットレディプロダクションちょこ札幌のオフィスは、女の子たちにとても評判が良いオフィスです。
「豪華で、高貴な気分になれる」なんて声もあります。
それもそのはず、今までにないような高環境実現のため、インテリアコーディネーターにデザインしていただきました。
しかし、豪華なだけではありません。
女の子を綺麗に見せるように、照明まで考えて作られているので、肌の美しさを最大限まで引き出すことができるお部屋なのです。
スタッフはどんな人?
高度な研修を受けた
安心の女性スタッフ在籍店

当店では、チャットレディの経験を積んだプロの女性スタッフが5名在籍しております。
当店では、チャットレディの経験を積んだプロの女性スタッフが5名在籍しております。更にスタッフ全員が以下の研修を、月に1回受けております。
・接客コミュニケーション研修
・ビジネスマナー研修
・セラピスト研修
・教え方研修
・メイク研修
ですので、スタッフの対応はもちろんの事、悩みや相談もお気軽に出来ます♪
また、お仕事のアドバイスは例を上げて説明してくれ、とてもわかりやすく的確で、稼げること確実です!!!
※監修元:
株式会社 青山プロダクション 青山夕香先生
チャットレディのお仕事に大切な
実生活でも使える会話術を紹介!
ちょこ札幌からメッセージ
ちょこ札幌は、女の子の負担を軽くして、札幌でチャットレディとして働きやすい環境を追求しています。
ちょこ札幌で働く女の子たちからの意見を大切にしながら、「こんなことができたらいいな、あんなものがあったらいいな」と日々考えています。
もちろんまだまだ完璧ではありませんが、ちょこ札幌で働きたいと思ってくれる女の子の夢を叶えるお手伝いがしたい!という気持ちは本物です。
この出会いがよい出会いになりますよう…心から願っております。
あなたからのお問い合わせを、お待ちしております。


- 面接交通費
2,000円
支給 - うれしい
入店祝金
最大10万 - 報酬最大
+212,000円
ボーナス